正方体中的几何常识，许多结论是需要我们理解并记忆的，以便于随时使用。

前言

正方体是非常特殊的图形，其中蕴含了很多常用的点、线、面的位置关系。

常识储备

如图所示，给定正方体\(ABCD-A\;'B\;'C\;'D\;'\)，如下的常用结论需要牢记：

(1). 三棱锥 \(B\;'-ACD\;'\) 是正四面体。三棱锥 \(D-ACD\;'\)

说明：三棱锥 \(B\;'-ACD\;'\) 的 \(6\) 条侧棱 \(B\;'D\;'\)、 \(B\;'A\)、 \(B\;'C\)、 \(AC\)、 \(AD\;'\) 和 \(CD\;'\) 都是正方体的面对角线；三棱锥 \(D-ACD\;'\) 的底面 \(ACD\;'\)的边是三条面对角线，三条侧棱是正方体的棱。

(2). 体对角线 \(B\;'D\perp\) 平面 \(ACD\;'\)

证法1：立体几何法，记体对角线\(B\;'D\)和平面\(ACD\;'\)的交点是\(N\)，

由 \(AC\perp BD\)，\(AC\perp BB\;'\)，$B'B\subsetneqq $平面 \(BDB\;'\)，$BD\subsetneqq $平面 \(BDB\;'\)，\(BB\;'\cap BD=\{B\}\)，则 \(AC\perp\) 平面 \(BDB\;'\)，则 \(AC\perp B\;'D\) ，即 \(B\;'D\perp AC\)；

同理，\(B\;'D\perp AD\;'\)，又由于 $AC\subsetneqq $平面 \(ACD\;'\)，$AD'\subsetneqq $平面 \(ACD\;'\)，\(AD\;'\cap AC=\{A\}\)，则 \(B\;'D\perp\)平面\(ACD\;'\)

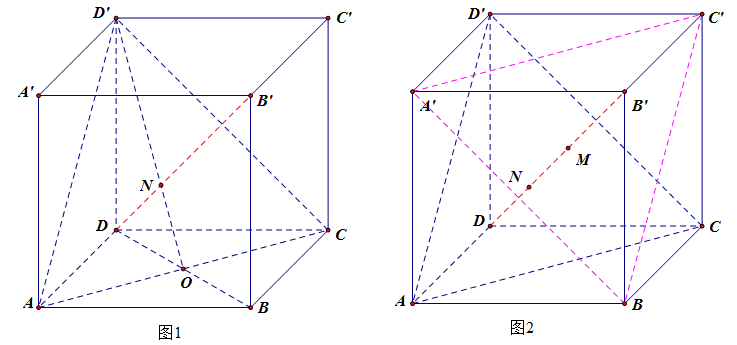
即体对角线 \(B\;'D\perp\) 平面 \(ACD\;'\)

证法2：空间向量法，

\(\overrightarrow{AC}\cdot\overrightarrow{B'D}=(\overrightarrow{AB}+\overrightarrow{BC})\cdot(\overrightarrow{B'B}+\overrightarrow{BD})\)

\(=\overrightarrow{AB}\cdot\overrightarrow{B'B}+\overrightarrow{AB}\cdot\overrightarrow{BD}+\overrightarrow{BC}\cdot\overrightarrow{B'B}+\overrightarrow{BC}\cdot\overrightarrow{BD}\)

\(=0+1\times\sqrt{2}\times(-\cfrac{\sqrt{2}}{2})+0+1\times\sqrt{2}\times\cfrac{\sqrt{2}}{2}=0\)，

即 \(\overrightarrow{AC}\perp\overrightarrow{B'D}\)，即 \(B'D\perp AC\)；

同理可得，\(B\;'D\perp AD\;'\)，又由于 $AC\subsetneqq $平面 \(ACD\;'\)，$AD'\subsetneqq $平面 \(ACD\;'\)，\(AD\;'\cap AC=\{A\}\)，

则 \(B\;'D\perp\)平面\(ACD\;'\)

(3). 平面\(ACD\;'//A\;'BC\;'\)(如图2)

(4). 平面\(ACD\;'\)与平面\(A\;'BC\;'\)的间距是\(\cfrac{1}{3}B\;'D\)，即体对角线的\(\cfrac{1}{3}\)(如图2)

(5). \(DN=\cfrac{1}{3}B\;'D\)(如图1，利用等体积法)

(6). 如果需要将正四面体或者墙角型的正三棱锥恢复还原为正方体，我们可以先画出正方体，然后在里面找出需要的正四面体或者墙角型正三棱锥。

(7). 圆内接正方形的中心就是圆心，正方形的对角线的长度就是圆的直径；球内接正方体的中心就是球心，正方体的体对角线的长度就是球的直径。

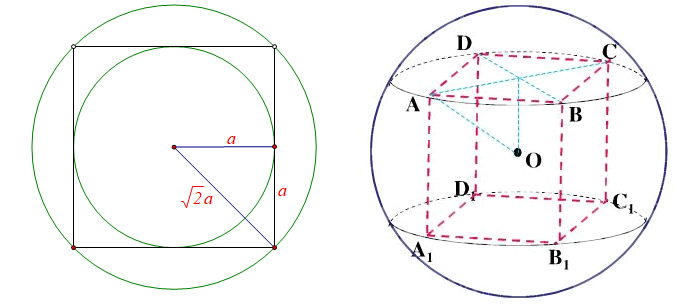
(8). 正方形的棱长设为\(2a\)，则正方形的内切圆半径为\(a\)，正方形的外接圆半径为\(\sqrt{2}a\)，三者的关系之比为\(2:1:\sqrt{2}\)；

正方体的棱长设为\(2a\)，则正方体的内切球半径为\(a\)，正方体的外接球半径为\(\sqrt{3}a\)，三者的关系之比为\(2:1:\sqrt{3}\)；

(9). 正三角形的棱长设为\(2a\)，则正三角形的内切圆半径为\(\cfrac{\sqrt{3}}{3}a\)，正三角形的外接圆半径为\(\cfrac{2\sqrt{3}}{3}a\)，三者的关系之比为\(2\sqrt{3}:1:2\)；

正四面体的棱长设为\(2a\)，则正四面体的内切球半径为\(\cfrac{\sqrt{6 }}{6}a\)，正四面体的外接球半径为\(\cfrac{\sqrt{6 }}{2}a\)，三者的关系之比为\(2\sqrt{6}:1:3\)；