引入
在一条链中,二叉查找树的时间复杂度就会退化成 \(O(n)\),这时我们就需要平衡树来解决这个问题。
\(Splay\)(伸展树)是平衡树的一种,它的每一步插入、查找和删除的平摊时间都是 \(O(\log n)\),出于对编程复杂度和算法性能的考虑,这是 OI 中常用的算法。
性质
\(Splay\) 本质上还是对二叉查找树的优化。所以它也具备二叉查找树的性质,即左子树任意节点的值 \(<\) 根节点的值 \(<\) 右子树任意节点的值。
操作
数组含义
| root | tot | fa[i] | ch[i][0] | ch[i][1] | val[i] | size[i] | cnt[i] |
|---|---|---|---|---|---|---|---|
| 根节点编号 | 节点数量 | 父节点编号 | 左儿子编号 | 右儿子编号 | 节点权值 | 子树大小 | 节点权值出现次数 |
基本操作
maintain(x):维护子树大小
void Splay::maintain(int x)
{
size[x] = size[ch[x][0]] + size[ch[x][1]] + cnt[x];
return ;
}
get(x):查询该节点是其父亲节点的左子树还是右子树
bool Splay::get(int x)
{
if( x == ch[fa[x]][1] )
return 1;
return 0;
}
clear(x):清理该节点
void Splay::clear(int x)
{
ch[x][0] = ch[x][1] = fa[x] = val[x] = size[x] = cnt[x] = 0;
return ;
}
旋转
旋转操作实际上是让某一个节点上移一个位置。
旋转操作需要保证,二叉查找树的性质不会改变,节点维护的信息依然正确,\(root\) 必须指向旋转后的根节点。
若节点 x 是其父亲的左节点

由于 \(x\) 的右儿子的权值大于 \(x\) 的权值,且 \(x\) 及其子树都属于 \(y\) 的左子树(即 \(x\) 的右子树实际上小于 \(y\) 的权值),所以我们将 \(x\) 的右子树改为 \(y\) 的左子树。
- 将 \(x\) 的右儿子变成 \(y\) 的左儿子,如果 \(x\) 有右儿子的话就让它的父亲变成 \(y\)。
ch[y][0] = ch[x][1]; fa[ch[x][1]] = y;
由于 \(y\) 及其子树的权值都大于 \(x\) 的权值,所以我们让 \(y\) 成为 \(x\) 的右儿子。
-
使 \(y\) 成为 \(x\) 的右儿子,\(x\) 变为 \(y\) 的父亲。
ch[x][chk^1] = y; fa[y] = x; -
如果 \(x\) 此时不是根节点,那么 \(x\) 将继承原先 \(y\) 作为 \(z\) 的儿子的位置(\(x\) 取代 \(y\) 成为 \(z\) 的左儿子或右儿子)。
fa[x] = z; if(z) ch[z][y == ch[z][1]] = x;

由此我们得到了节点 \(x\) 上升一个位置的树,显然,这棵树仍然满足二叉搜索树的性质。
实现
void Splay::rotate(int x)
{
int y = fa[x],z = fa[y],chk = get(x);
ch[y][chk] = ch[x][chk ^ 1];
if( ch[x][chk ^ 1] )
fa[ch[x][chk ^ 1]] = y;
ch[x][chk ^ 1] = y;
fa[y] = x;
fa[x] = z;
if(z)
ch[z][y == ch[z][1]] = x;
maintain(y);
// 要先维护 y 的子树大小
// 因为现在 y 是 x 的儿子
maintain(x);// 别忘了维护子树大小
return ;
}
代码中采用异或来实现左右不同旋转情况,当然我们可以写两个函数分别来实现左旋和右旋。
伸展
伸展操作是在保持伸展树性质的前提下,将节点 \(x\) 转移到根节点。在这个转移过程中,我们分为三种情况。
首先我们设节点 \(x\) 的父节点为节点 \(y\),若节点 \(y\) 有父节点,其父节点为 \(z\)。
第一种情况:\(y\) 是根节点
- 若 \(x\) 是 \(y\) 的左儿子,我们进行一次右旋操作
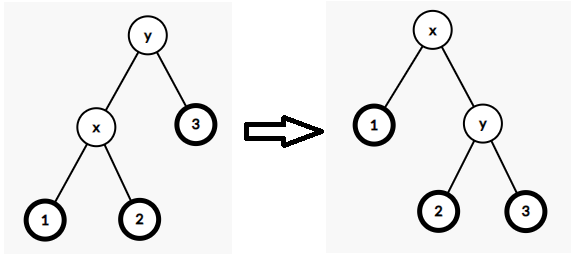
- 若 \(x\) 是 \(y\) 的右儿子,我们进行一次左旋操作
第二种情况:\(y\) 不是根节点,且 \(x\) 和 \(y\) 同为左儿子或右儿子
- 若 \(x\) 和 \(y\) 同时是各自父节点的左儿子,则进行两次右旋操作
- 若 \(x\) 和 \(y\) 同时是各自父节点的右儿子,则进行两次左旋操作
第三种情况:\(y\) 不是根节点,且 \(x\) 和 \(y\) 一个为左儿子一个为右儿子
- 若 \(x\) 是 \(y\) 的左儿子,\(y\) 是 \(z\) 的右儿子,则进行一次右旋 - 左旋操作
- 若 \(x\) 是 \(y\) 的右儿子,\(y\) 是 \(z\) 的左儿子,则进行一次左旋 - 右旋操作
实现
void Splay::splay(int x)
{
for(int i = fa[x];i = fa[x],i; rotate(x))
if( fa[i] )
{
if( get(x) == get(i) )
rotate(i);
else
rotate(x);
}
root = x;
return ;
}
插入
-
如果树为空,则直接插入根节点
-
如果找到了一个节点权值与插入权值相等,则增大该节点并维护信息,再进行 Splay 操作
-
否则接着往下找,要是找到空节点就直接插入
实现
void Splay::insert(int v)
{
if( root == 0 )
{
tot ++;
val[tot] = v;
cnt[tot] ++;
root = tot;
maintain(root);
return ;
}
int cur = root,x = 0;
while(1)
{
if( val[cur] == v )
{
cnt[cur] ++;
maintain(cur);
maintain(x);
splay(cur);
break;
}
x = cur;
cur = ch[cur][val[cur] < v];
if( cur == 0 )
{
tot ++;
val[tot] = v;
cnt[tot] ++;
fa[tot] = x;
ch[x][val[x] < v] = tot;
maintain(tot);
maintain(x);
splay(tot);
break;
}
}
}
寻找数 \(x\) 的排名(比它小的数的个数值 + 1)
-
若 \(x\) 小于当前节点权值,则向左子树查找
-
若 \(x\) 大于当前节点权值,则答案加上左子树大小
size[i]和当前节点权值出现次数cnt[i] -
若找到与 \(x\) 相等的节点,则返回当前答案 \(+ 1\)
实现
int Splay::find_rank(int v)
{
int ans = 0,cur = root;
while(1)
{
if( v < val[cur] )
cur = ch[cur][0];
else
{
ans += size[ch[cur][0]];
if( v == val[cur] )
{
splay(cur);
return ans + 1;
}
ans += cnt[cur];
cur = ch[cur][1];
}
}
}
寻找排名为 \(x\) 的数的值
\(v\) 表示剩余排名,在初始排名的条件下不断减少。
-
若左子树不为空且剩余排名 \(v\) 小于等于左子树大小 \(size\)(即 \(x\) 在左子树),向左子树查找
-
否则减去左子树大小和根的出现次数作为剩余排名 \(v\)。若 \(v\leq 0\),则返回根节点,否则向右子树查找。
实现
int Splay::find_num(int v)
{
int cur = root;
while(1)
{
if( ch[cur][0] != 0 && v <= size[ch[cur][0]] )
cur = ch[cur][0];
else
{
v -= cnt[cur] + size[ch[cur][0]];//.//
if( v <= 0 )
{
splay(cur);
return val[cur];
}
cur = ch[cur][1];
}
}
}
查询前驱(小于 \(x\) 的最大的数)
先插入节点 \(x\),这样 \(x\) 就处在了根节点的位置。
此时 \(x\) 的左子树都小于 \(x\),寻找 \(x\) 的左子树的最右边节点即小于 \(x\) 的最大的数。
实现
int Splay::pre()
{
int cur = ch[root][0];
if( cur == 0 )
return cur;
while( ch[cur][1] )
cur = ch[cur][1];
splay(cur);
return cur;
}
查询后继(大于 \(x\) 的最小的数)
基本思想与查询前驱相同。
先插入节点 \(x\),这样 \(x\) 就处在了根节点的位置。
此时 \(x\) 的右子树都大于 \(x\),寻找 \(x\) 的右子树的最左边节点即大于 \(x\) 的最小的数。
实现
int Splay::next()
{
int cur = ch[root][1];
if( cur == 0 )
return cur;
while( ch[cur][0] )
cur = ch[cur][0];
splay(cur);
return cur;
}
合并
对于合并两棵树,其中一棵树的值都小于另一棵树的值。
我们可以找到较小一棵树的最大值 \(x\),将其旋转到根节点。
再把较大一棵树作为 \(x\) 的右子树插入。
删除
-
首先将 \(x\) 转移到根节点
-
若 \(x\) 值不只一个,即 \(cnt[x] > 1\),则直接减一退出即可。
-
否则将它的左右两棵子树合并
实现
void Splay::del(int v)
{
find_rank(v);/////
if( cnt[root] > 1 )
{
cnt[root] --;
maintain(root);
return ;
}
if( ch[root][0] == 0 && ch[root][1] == 0 )
{
clear(root);
root = 0;
return ;
}
if( ch[root][0] == 0 )
{
int cur = root;
root = ch[root][1];
fa[root] = 0;
clear(cur);
return ;
}
if( ch[root][1] == 0 )
{
int cur = root;
root = ch[root][0];
fa[root] = 0;
clear(cur);
return ;
}
int cur = root;
int x = pre();
fa[ch[cur][1]] = x;
ch[x][1] = ch[cur][1];
clear(cur);
maintain(root);
return ;
}
模板题
Luogu P3369 【模板】普通平衡树
完整代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 114514;
int n;
int root;
// 根节点
int ch[MAXN][2],fa[MAXN];
// 子节点( 0 左 1 右 ) 父节点
int val[MAXN];
// 权值
int size[MAXN];
// 子树大小
int cnt[MAXN];
// 这个权值出现的次数
int tot;
// 节点个数
struct Splay{
void maintain(int x);
// 维护子树大小
bool get(int x);
// 查找这个节点是父亲的左子树还是右子树
void clear(int x);
// 销毁这个节点
void rotate(int x);
// 旋转
void splay(int x);
// 伸展操作
void insert(int v);
// 插入数 v
int find_rank(int v);
// 查询数 v 的排名
int find_num(int v);
// 查询排名为 v 的数
int pre();
// 查询根节点的前驱
int next();
// 查询根节点的后继
void del(int v);
// 删除 v
}tree;
void Splay::maintain(int x)
{
size[x] = size[ch[x][0]] + size[ch[x][1]] + cnt[x];
return ;
}
bool Splay::get(int x)
{
if( x == ch[fa[x]][1] )
return 1;
return 0;
}
void Splay::clear(int x)
{
ch[x][0] = 0;
ch[x][1] = 0;
fa[x] = 0;
val[x] = 0;
size[x] = 0;
cnt[x] = 0;
return ;
}
void Splay::rotate(int x)
{
int y = fa[x],z = fa[y],chk = get(x);
ch[y][chk] = ch[x][chk ^ 1];
if( ch[x][chk ^ 1] )
fa[ch[x][chk ^ 1]] = y;
ch[x][chk ^ 1] = y;
fa[y] = x;
fa[x] = z;
if(z)
ch[z][y == ch[z][1]] = x;
maintain(y);
maintain(x);
return ;
}
void Splay::splay(int x)
{
for(int i = fa[x];i = fa[x],i; rotate(x))
if( fa[i] )
{
if( get(x) == get(i) )
rotate(i);
else
rotate(x);
}
root = x;
return ;
}
void Splay::insert(int v)
{
if( root == 0 )
{
tot ++;
val[tot] = v;
cnt[tot] ++;
root = tot;
maintain(root);
return ;
}
int cur = root,x = 0;
while(1)
{
if( val[cur] == v )
{
cnt[cur] ++;
maintain(cur);
maintain(x);
splay(cur);
break;
}
x = cur;
cur = ch[cur][val[cur] < v];
if( cur == 0 )
{
tot ++;
val[tot] = v;
cnt[tot] ++;
fa[tot] = x;
ch[x][val[x] < v] = tot;
maintain(tot);
maintain(x);
splay(tot);
break;
}
}
}
int Splay::find_rank(int v)
{
int ans = 0,cur = root;
while(1)
{
if( v < val[cur] )
cur = ch[cur][0];
else
{
ans += size[ch[cur][0]];
if( v == val[cur] )
{
splay(cur);
return ans + 1;
}
ans += cnt[cur];
cur = ch[cur][1];
}
}
}
int Splay::find_num(int v)
{
int cur = root;
while(1)
{
if( ch[cur][0] != 0 && v <= size[ch[cur][0]] )
cur = ch[cur][0];
else
{
v -= cnt[cur] + size[ch[cur][0]];//.//
if( v <= 0 )
{
splay(cur);
return val[cur];
}
cur = ch[cur][1];
}
}
}
int Splay::pre()
{
int cur = ch[root][0];
if( cur == 0 )
return cur;
while( ch[cur][1] )
cur = ch[cur][1];
splay(cur);
return cur;
}
int Splay::next()
{
int cur = ch[root][1];
if( cur == 0 )
return cur;
while( ch[cur][0] )
cur = ch[cur][0];
splay(cur);
return cur;
}
void Splay::del(int v)
{
find_rank(v);/////
if( cnt[root] > 1 )
{
cnt[root] --;
maintain(root);
return ;
}
if( ch[root][0] == 0 && ch[root][1] == 0 )
{
clear(root);
root = 0;
return ;
}
if( ch[root][0] == 0 )
{
int cur = root;
root = ch[root][1];
fa[root] = 0;
clear(cur);
return ;
}
if( ch[root][1] == 0 )
{
int cur = root;
root = ch[root][0];
fa[root] = 0;
clear(cur);
return ;
}
int cur = root;
int x = pre();
fa[ch[cur][1]] = x;
ch[x][1] = ch[cur][1];
clear(cur);
maintain(root);
return ;
}
int main()
{
scanf("%d",&n);
for(int i = 1,opt,x;i <= n; i++)
{
scanf("%d%d",&opt,&x);
if( opt == 1 )
tree.insert(x);
else if( opt == 2 )
tree.del(x);
else if( opt == 3 )///
printf("%d\n",tree.find_rank(x));
else if( opt == 4 )////
printf("%d\n",tree.find_num(x));
else if( opt == 5 )
{
tree.insert(x);
printf("%d\n",val[tree.pre()]);
tree.del(x);
}
else
{
tree.insert(x);
printf("%d\n",val[tree.next()]);
tree.del(x);
}
}
return 0;
}

