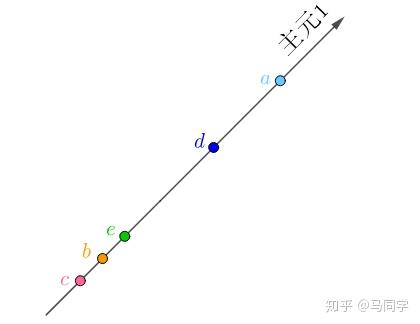
一、主成分分析
1、动机:多个变量之间往往存在一定的相关性,可以通过线性组合的方式从中提取信息。
2、主成分分析:将原始的n维数据投影到低维空间,并尽可能的保留更多的信息。
---投影后方差最大
---最小化重构误差
从而达到降维的目的:使用较少的主成分得到较多的信息。
二、图像解释
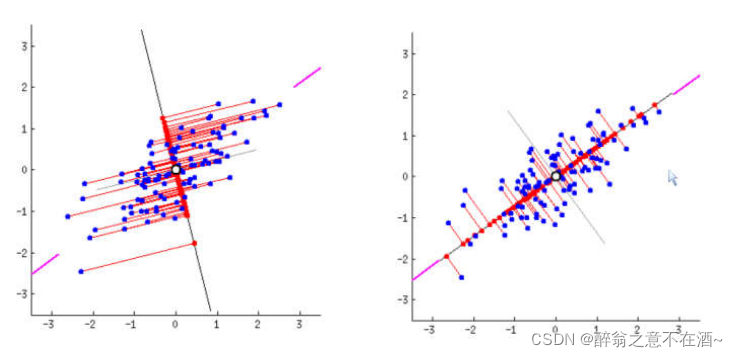
比如我们想把二维数据降维到一维,那么我们要去找到一条线使得投影后方差最大,如二图中的直线,然后我们把二维的点都投影到这条线上,此时线上的投影点既是我们降维后得到的数据,那么我们该如何实现这个操作?
三、底层算法
1、原理

2、案例

3、代码实现
def pca(X,k):
m_samples , n_features = X.shape
#中心化 去均值 均值为0
mean = np.mean(X,axis=0)
normX = X - mean #去均值,中心化
cov_mat = np.dot(np.transpose(normX),normX) #协方差矩阵
#对二维数组的transpose操作就是对原数组的转置操作 矩阵相乘
vals , vecs = np.linalg.eig(cov_mat) #得到特征向量和特征值
print('特征值',vals)
print('特征向量',vecs)
eig_pairs = [(np.abs(vals[i]),vecs[:,i]) for i in range(n_features)]
print(eig_pairs)
print('-------------')
#将特征值由大到小排列
eig_pairs.sort(reverse=True)
print(eig_pairs)
print('-------------')
feature = np.array(eig_pairs[0][k])
print(feature)
#将数据进行还原操作 normX 中心化后的数据 和 特征向量相乘
data = np.dot(normX,np.transpose(feature))
return data
X = np.array([[-1,1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
data = pca(X,1)
print(data)
4、在sklearn中调用
from sklearn.decomposition import PCA
p = PCA(n_components=1)
a = p.fit_transform(X)
print(a)
四、PCA算法总结
作为一个非监督学习的降维方法,它只需要特征值分解,就可以对数据进行压缩,去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点,出现了很多PCA的变种,比如非线性降维的KPCA,还有解决内存限制的增量PCA方法Incremental PCA,以及解决稀疏数据降维的PCA方法Sparse PCA等。
PCA算法的主要优点有:
(1)仅仅需要以方差衡量信息量,不受数据集以外的因素影响。
(2)各主成分之间正交,可消除原始数据成分间的相互影响的因素。
(3)计算方法简单,主要运算是特征值分解,易于实现。
PCA算法的主要缺点有:
(1)主成分各个特征维度的含义具有一定的模糊性, 不如原始样本特征的解释性强。
(2)方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据
处理有影响。
————————————————
https://zhuanlan.zhihu.com/p/77151308
https://www.zhihu.com/question/41120789?utm_source=qq 【great】
主元分析也就是PCA,主要用于数据降维。
1 什么是降维?
比如说有如下的房价数据:
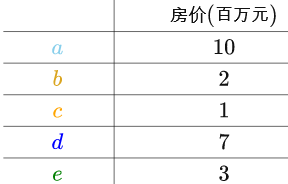
实数轴上:
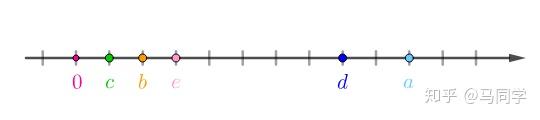
不过数据还需要处理下,假设房价样本用X表示,那么均值为:
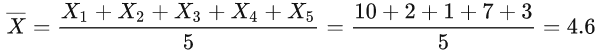
然后以均值为原点:
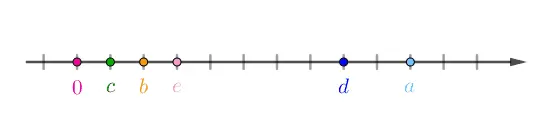
以X bar为原点的意思是,以X bar为0,那么上述表格的数字就需要修改下:

这个过程称为“中心化”。“中心化”处理的原因是,这些数字后继会参与统计运算,比如求样本方差,中间就包含了
:
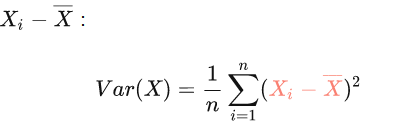
说明下,虽然样本方差的分母是应该为n-1,这里分母采用n是因为这样算出来的样本方差为一致估计量,不会太影响计算结果并且可以减小运算负担。
用“中心化”的数据就可以直接算出“房价”的样本方差:
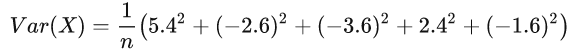
“中心化”之后可以看出数据大概可以分为两类:
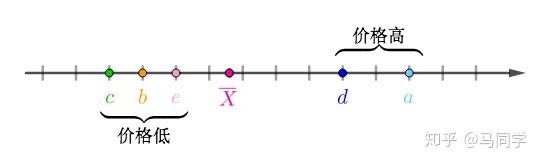
现在新采集了房屋的面积,可以看出两者完全正相关,有一列其实是多余的:
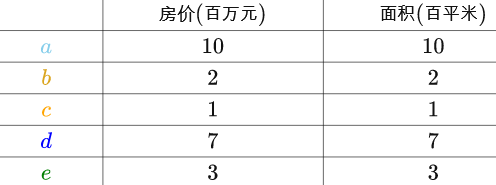
求出房屋样本、面积样本的均值,分别对房屋样本、面积样本进行“中心化”后得到:
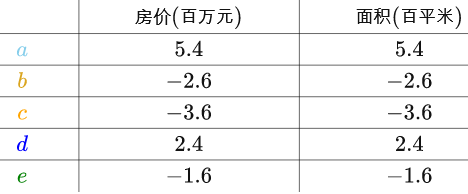
房价(X)和面积(Y)的样本协方差是这样的(这里也是用的一致估计量):
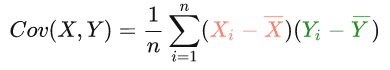
可见“中心化”后的数据可以简化上面这个公式,这点后面还会看到具体应用。
把这个二维数据画在坐标轴上,横纵坐标分别为“房价”、“面积”,可以看出它们排列为一条直线:
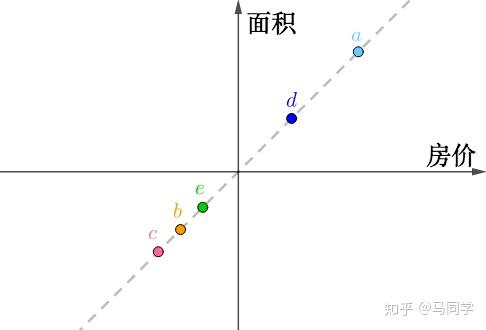
如果旋转坐标系,让横坐标和这条直线重合:
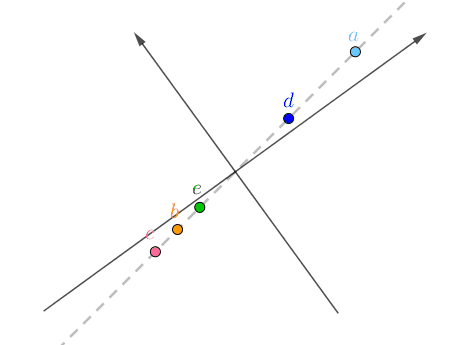
旋转后的坐标系,横纵坐标不再代表“房价”、“面积”了,而是两者的混合(术语是线性组合),这里把它们称作“主元1”、“主元2”,坐标值很容易用勾股定理计算出来,比如
在“主元1”的坐标值为:
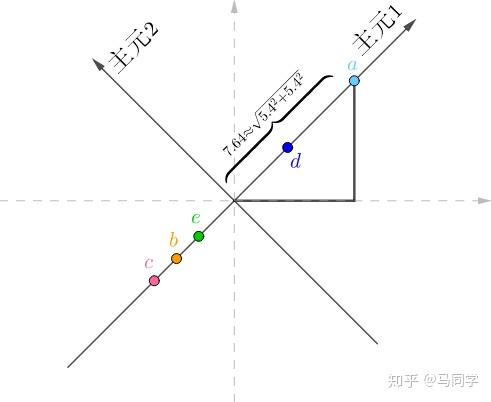
很显然,在“主元2”上的坐标为0,把所有的房间换算到新的坐标系上:
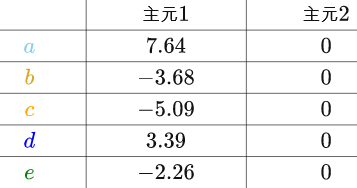
因为“主元2”全都为0,完全是多余的,我们只需要“主元1”就够了,这样就又把数据降为了一维,而且没有丢失任何信息(?????):